Dua jenis toleransi secara umum dapat dinyatakan dala dua bentuk:
- Bilateral toleransi (Toleransi dua sisi)
Dinyatakan dalam bentuk plus-minus dari nilai rata-rata atau spesifikasi yang dipersyaratkan.
Contoh Standar tekanan ban mobil sebesar 35 ±5 kg/m2, artinya data yang ada diantara 30-40 kg/m2
2. Unilateral toleransi (toleransi satu sisi)
Metoda toleransi yang menggunakan deviasi dari satu sisi, apakah itu plus atau minus dari specified dimension
Contoh nilai runout, flatness, silindrisitas, kekuatan luluh, nilai tegangan tarik logam. Tidak mungkin terdapat nilai runout , kedataran atau kekuatan las di bawah 0 atau minus. Jadi satu sisi saja yang dijadikan indicator evaluasi.
Ilustrasi Toleransi Satu Sisi pada Kekuatan Lasan
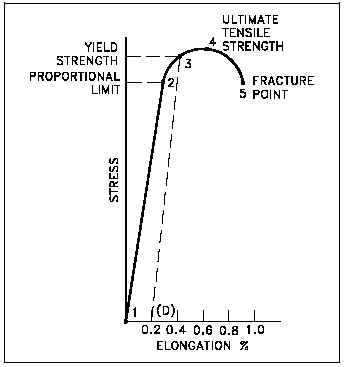
Nilai kekuatan lasan diperoleh dengan melakukan uji tarik sampai benda ujinya patah, produk akan patah bila diberikan tegangan tarik yang melebihi batas kekuatan logam (ada tegangan yang diberikan), hal ini akan ditandai seperti graphik di samping, artinya nilai kekuatan lasan akan mempunyai nilai lebih besar dari 0
Nilai Cp
Cp menyatakan perbandingan antara lebar spesifikasi dibanding dengan lebar variasi
Index Capability = Besar Spesifikasi / Besar Variasi = (USL-LSL)/(6 x sigma)
Agar lebih dipahami dalam menghitung Cp, maka perhatikan graphik di bawah ini mengenai variasi dan spesifikasi
Maka kita bisa menghitung Cp kekerasan hasil lasan sebesar:
Menghitung Cp untuk unilateral toleransi (toleransi satu sisi)
Misalkan:
- standard minimum lasan (LSL) = 29,4 kN
- dengan kata lain USL tidak terdefinisi atau tidak bisa ditentukan karena bisa mempunyai nilai sebesar-besarnya atau semaksimal mungkin atau ~ kN ( boleh sampai tak terhingga), maka USL = ~ kN
- Data dari 31 test uji hasil lasan yang diambil 1 pc tiap 1000 pcs lasan bervariasi dari minimum 34 kn sampai dengan 80 kN
Ilustrasi graphiknya
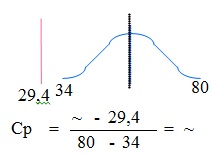
Nilai ~ mempunyai pengertian nilai tersebut tidak terdefinisi/ tidak ada, bila kita gunakan Software Minitab, maka nilai Cp dinyatakan dengan tanda * (tidak ada).
Kita juga mengetahui kalau dalam pecahan matimatika bila penyebutnya adalah nol atau tak terhingga (~) atau nilai pembilangnya adalah ~ maka dikatakan bahwa nilai pecahan tersebut tidak terdefinisi / tidak bisa ditentukan.
Jadi untuk menghitung Cp diperlukan 2 spesifikasi (spesifikasi atas dan spesifikasi bawah). jika hanya ada satu spesifikasi, maka lebar specifikasinya tidak bisa diketahui
Untuk nilai Cpk
Selain menyatakan perbandingan antara lebar spesifikasi dengan lebar variasi, Cpk juga menggambarkan posisi variasi terhadap spesifikasi.
Indek Capability = [Posisi Variasi terhadap spec atas atau bawah]Min/(1/2 Lebar variasi)
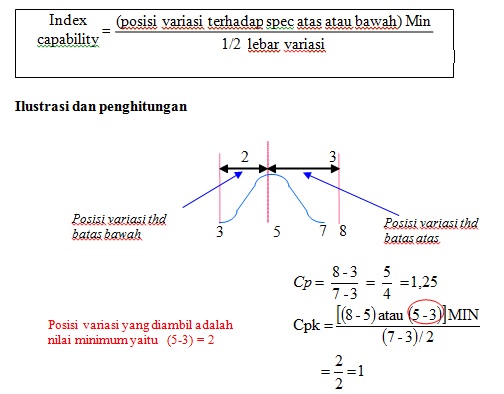
Cpk Satu Toleransi
Untuk kasus Toleransi Satu Sisi, misalkan didapat nilai rata-rata kekuatan las / Nilai tengah (X) = 53,2 kN, data nilai tengah diambil dari data dari 31 test uji hasil lasan, yang diambil 1 pc tiap 1000 pcs lasan , nilai mempunyai bervariasi dari 34 kn sampai dengan 80 kN, minimum persyaratan (LSL) = 29,4 kN
maka Cpknya bisa dihitung, kalau sebelumnya menggunakan posisi variasi paling dekat ke spesifikasi atas atau bawah, sekarang karena hanya ada satu toleransi, maka langsung dihitung posisi variasinya terhadap toleransi, sehingga semakin tinggi Cpk, semakin jauh variasinya dari spesifikasi, artinya proses semakin baik.

Dari cara penghitungan di atas terlihat apabila nilai rata-rata / nilai tengah (X) bertambah besar , maka nilai PV akan bertambah besar, karena PV berbanding lurus dengan Cpk, maka nilai Cpk pun bertambah besar, atau dikatakan proses semakin baik
Aplikasi Minitab
Data aplikasi minitab yang saya kondisikan sesuai dengan pertanyaan bapak. Misalkan terdapat masing-masing terdapat 31 data untuk dua kelompok hasil lasan dengan minimum kekuatan 29,4 kN, sebagai berikut:
|
No |
Weld Strength-1 | Weld Strength-2 | No | Weld Strength-1 |
Weld Strength-2 |
|
| 1 | 53,2 | 70,2 | 16 | 50,0 | 78,8 | |
| 2 | 54,0 | 78,7 | 17 | 50,0 | 77,8 | |
| 3 | 55,0 | 79,2 | 18 | 50,9 | 79,0 | |
| 4 | 53,3 | 77,5 | 19 | 55,0 | 78,4 | |
| 5 | 53,7 | 78,3 | 20 | 54,9 | 77,8 | |
| 6 | 53,5 | 78,8 | 21 | 53,2 | 78,8 | |
| 7 | 54,2 | 78,7 | 22 | 53,4 | 78,7 | |
| 8 | 54,3 | 77,6 | 23 | 50,0 | 78,8 | |
| 9 | 53,7 | 78,9 | 24 | 53,8 | 79,1 | |
| 10 | 55,0 | 77,6 | 25 | 53,7 | 78,2 | |
| 11 | 53,9 | 77,8 | 26 | 50,0 | 77,5 | |
| 12 | 55,0 | 78,3 | 27 | 54,3 | 79,1 | |
| 13 | 54,7 | 78,2 | 28 | 53,4 | 78,4 | |
| 14 | 54,0 | 77,3 | 29 | 50,0 | 78,8 | |
| 15 | 53,5 | 78,4 | 30 | 54,3 | 79,1 | |
| 31 | 52,0 | 77,4 |
Unit = kN
Hasil penghitungan dengan software minitab:
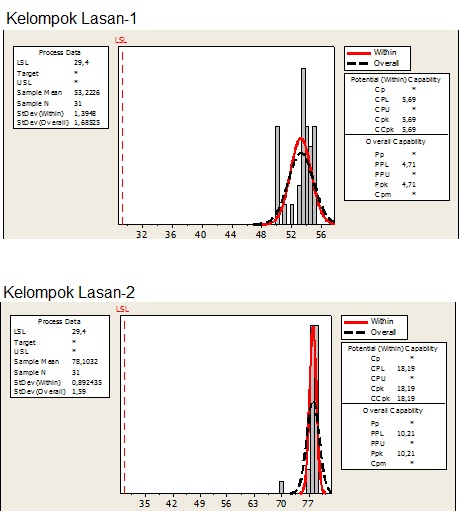
Saya sumarikan dari kedua graphik dalam bentuk tabel seperti di bawah ini:
| Kelompok Lasan | Nilai rata2 (Nilai Tengah) | Nilai Cpk | Nilai Cp |
| Lasan pertama | 53,2 kN | 5,69 | * |
| Lasan kdua | 78 kN | 18,19 | * |
Dari tabel di atas jelas terlihat semakin besar nilai rata-ratanya (Nilai tengah) maka akan semakin besar nilai Cpk nya, juga terlihat jelas bahwa nilai Cp ditandai dengan * (atau tidak didefinisikan)
Selamat mencoba & Semoga membantu
www.improvementqhse.com